前一天介紹完了一般的Decision Tree，而今天要來講另外一種Decision Tree—CART Tree（Classification And Regression Tree）。從CART Tree的名字來看就知道，CART Tree具有分類（Classification）和迴歸（Regression）兩種功能。一般的Decision Tree決定分類的依據是entropy，而CART Tree的分類依據是採用Gini Index（吉尼係數）。另外最大的不同處在於，用entropy分類的Decision Tree可以分化成多個節點，而使用Gini Index分類的CART Tree則只能分化成兩個節點。

先來看看什麼是Gini Index，下方是Gini Index的算法，p為正確（True）的機率、q為錯誤（False）的機率。Gini Index的數值介於0和1之間，越接近1代表分配的越不平均（集中於一邊）、越接近0則代表分配的越平均。

接下來我們就來看看CART Tree是怎麼運作的吧！我們同樣用前一天的例子來說，假設一開始有十次決定出門和十次決定不出門的資料，如果我們用是假日還是平日去分類的話，有4個不出門和6個出門被分到平日、6個不出門和4個出門分到假日。平日的Gini Index會是0.42 + 0.62 = 0.52、而假日的Gini Index則是0.62 + 0.42 = 0.52，加權過後是(10 / 20) * 0.52 + (10 / 20) * 0.52 = 0.52。

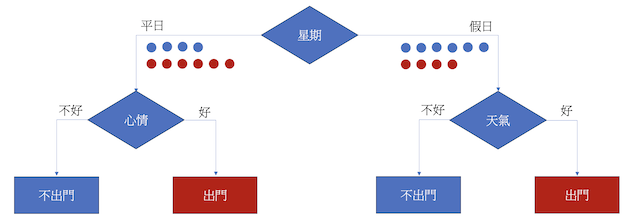
從上方的例子獲得加權的Gini Index過後，演算法會自動再去計算不同分類的Gini Index，最終選擇Gini Index最大的作為最後的最佳解。